快速DIC形变测试技术与工程应用
1李得睿 2陈卫红 2彭波 3晏班夫
(1上海交通大学船舶海洋与建筑工程学院,上海,200240;2北京智博联科技股份有限公司,北京 100088;3湖南大学土木工程学院,长沙,410082)
[摘 要] 数字图像相关(Digital image correlation, DIC)技术以其亚像素级别测试精度、可远距多点非接触测试、设备简单、操作简便等特点,在结构形变测试中受到较多关注。本研究采用基于傅里叶变换的互相关(Fourier transform-based cross correlation, FTCC)算法与反向组合高斯牛顿 (Inverse Compositional Gauss–Newton, IC-GN)算法的DIC运算框架,对DIC在工程应用中的可行性进行分析。通过精度分析以及实际工程应用案例,对基于FTCC和IC-GN算法的DIC计算架构进行测试,结果表明DIC技术在工程应用中的测试精度有理论保证,且得到了较好的实测结果。
[关键词] 数字图像相关;形变测试;亚像素匹配
Rapid DIC Deformation Measurement Technology and Engineering Application
1Li Derui 2Chen Weihong 2Peng Bo 3Yan Banfu
(1 School of Naval and Architectural , Ocean & Civil Engineering, Shanghai Jiaotong University ,Shanghai,200240; 2 Beijing ZBL Science & Technology Co. Ltd.,Beijing 100088; 3 College of Civil Engineering, Hunan University, Changsha,410082)
Abstract: Digital image correlation technology has attracted more attention in structural deformation test because of its sub-pixel level test accuracy, remote multi-point non-contact test, simple equipment and easy operation. In this study, DIC operation framework based on cross-correlation algorithm of Fourier transform and inverse Compositional Gauss-Newton algorithm is used to analyze the feasibility of DIC in engineering application. Through the accuracy analysis and practical engineering application cases, the DIC computing architecture based on FTCC and IC-GN algorithm is tested. The results show that DIC technology has theoretical guarantee for the test accuracy in engineering application, and good measurement results are obtained.
Keywords: digital image correlation; deformation measurement; subpixel matching
前 言
形变测试是研究各类土木工程材料与结构特性的重要手段。传统形变测试方法普遍存在现场操作困难、多点测试不便、测试成本高、需人造靶标、测试效率低下等问题。在结构测试领域,近年来数字图像相关(Digital image correlation, DIC)方法以其亚像素级别测试精度、可远距多点非接触测试、设备简单、操作简便等特点,在结构形变测试中受到较多关注
[1-3]。
依据算法原理,可将DIC技术分为局部DIC技术
[4]与全局DIC技术
[5], [6];依据拍摄原理,又可将局部DIC技术分为二维局部DIC技术
[7]、立体局部DIC技术
[8], [9]与数字体积相关(Digital Volume Correlation, DVC)技术
[10]。其中,全局DIC技术并非主流DIC技术,目前大部分学术论文内容以及几乎所有商业DIC软件均基于局部DIC技术实现;而立体局部DIC技术与二维局部DIC技术并无本质区别,立体局部DIC技术需要进行多相机组的外参数标定,来实现三维位移的测量,其本身仍运行二维局部DIC的算法;DVC技术实质上是DIC技术的三维拓展,其基于类似X射线对物体进行三维扫描,得到物体的三维实验数据,运行二维DIC算法的三维拓展版本,实现对物体内部的三维运动测试,DVC难以在土木工程测试领域推广,其所需设备非常规设备,并且大部分土木工程测试情景不需要运用DVC进行三维体积位移追踪。基于此,本文主要基于二维局部DIC技术,进行土木工程结构位移测试的研究与可行性分析。为了方便表述,本文一律将二维局部DIC技术称之为DIC技术。
晏班夫等
[3]为减少基于快速归一化互相关(Fast normalized cross correlation, FNCC)
[11]的整像素并行搜索算法的运算量,基于CUDA 并行计算平台,使用消费级NVIDIA GPU 显卡,将图像配准领域广泛应用的基于快速傅里叶变换的互相关(Fourier transform-based cross correlation,FTCC)
[12]整像素初值搜索算法引入GPU-DIC并行运算框架中,大大提升了初值搜索速度,结合反向组合高斯-牛顿(Inverse compositional Gauss–Newton,IC-GN)
[13]亚像素算法,位移测试达到了与传统FNCC并行算法相当的精度与稳定性主要,通过实验室实验证明了DIC在土木工程形变测试领域的实用性。
本文主要采用理论精度分析与现场实验对集成FTCC和IC-GN算法的DIC计算架构进行测试,以验证该测试体系以及测试系统在工程应用场景下,尤其是土木工程室外场景下结构位移测试的可行性。实验结果表明,该DIC计算架构具备在土木工程室外场景下的测试可行性。
1 原理简介
1.1 硬件系统
图 1为典型的数字图像检测系统,主要由笔记本电脑(计算设备)、数字图像采集仪、被测物以及照明设备(光源)等硬件设备及数字图像测量软件组成,其中数字图像测量软件是核心。图2为基于GPU并行运算的快速DIC形变测试研究框架及流程,其中DIC技术的核心算法包括整像素初值搜索算法(FNCC及FTCC)与亚像素匹配算法(IC-GN与FA-NR)。亚像素算法中应用最广泛的是基于形函数的迭代型算法,例如IC-GN、FA-NR等。得到的位移场经过差分及平滑可以得到应变场,这部分内容在本文并未涉及。

图 1 数字图像检测系统基本构成

图 2 ZNCC遍历运算示意图
1.2 DIC整像素算法
1.2.1 传统FNCC算法
如图 2所示,
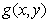
是尺寸为

像素的搜索区域,也即匹配图像模板。从搜索区域中截取出其中蓝色虚线区域,作为引用子集
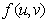
,引用子集尺寸为
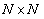
像素,
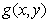
中黄色实线区域尺寸与引用子集
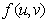
尺寸相同。整像素搜索的核心目标,即定量地找出
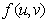
的中心点,在
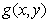
中的整像素坐标
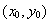
该坐标也就是整像素初值搜索的结果。容易想到,将
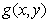
中与引用子集
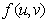
尺寸相同的黄色实线区域,作为目标区域,从左至右、从上到下地逐个像素点遍历全部的
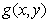
,在每个遍历路径上的像素点处,将目标区域与
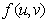
做式的ZNCC运算,即
其中,
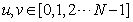
,
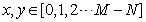
,
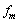
为
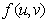
的灰度均值,
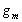
为
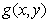
中黄色实线目标区域的灰度均值,
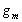
随
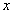
与
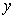
的变化而发生改变。
遍历过后,即得到一个
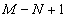
维的
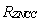
系数方阵,该方阵中,假设
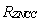
最大值处的坐标为
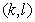
,则整像素初值搜索结果
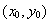
为
可以看到,由式直接表述的ZNCC遍历算法,至少需要
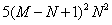
次加法运算与
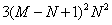
次乘法运算,且计算机乘法运算耗时远大于加法运算。在实际DIC形变测试中,一般有,
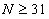
,
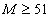
,式的运算量随着
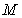
的增大,呈平方倍增长,随着
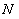
的增大,呈4次方趋势增长。由此可知,式的直接实现方式并非高效。
Lewis
[11]于1995年提出了快速归一化互相关(Fast normalized cross correlation, FNCC)整像素初值搜索算法,FNCC算法即式的快速算法。FNCC将式的分子基于快速傅里叶变换进行计算,采用图像积分表快速计算式的分母部分。
实际运用FNCC算法进行整像素初值搜索时,
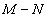
的值代表了搜索范围,
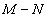
越大,则FNCC的搜索能力越强,但相对应的运算量也就越大,且运算量随着
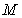
与
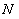
的增大呈非线性快速增长。
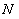
越大则意味着做相关运算的数据越多,也即鲁棒性越强,
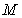
越大则意味着搜索范围越广,增大了受干扰的可能性,也即鲁棒性变差。实际运算时,
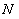
的取值范围一般为15-71,普遍取
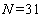
。
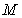
的取值可表示为
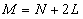
,
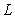
表示搜索范围,单位为像素,
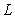
的大小则随测试情况而定。
若两帧图像间,被测物位移变化较大,如混凝土加载试验中,混凝土梁临近破坏前的最后几帧图像,由于混凝土梁此时刚度很小,所以两帧图像间混凝土梁的变位较大,
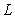
取50也有可能达不到相应的搜索范围要求,且此时FNCC计算量非常大,鲁棒性也受到较大影响。由于土木工程测试情形,普遍具备小位移、慢位移、小旋转的特点,FNCC算法还是能够满足绝大多数土木工程形变测试场景的。在进行高速冲击试验时,则需要运用高速摄像机进行图像的采集,来实现两帧间小位移的条件。
1.2.2 FTCC算法
针对土木工程试验中的大刚体位移情形,晏班夫等
[3]引入基于傅里叶变换的互相关(Fourier transform-based cross correlation, FTCC)算法,作为DIC整像素初值搜索算法,并证实了FTCC算法可实现DIC技术在大刚体位移情形下的快速计算。
FTCC被Reddy等
[12]提出后,被广泛用于计算视觉中的图像配对与校准工作,潘兵等
[13]将FMT-CC引入RG-DIC算法中,实现了目标物存在较大平移、旋转情形下的初值搜索。FTCC算法利用引用子集
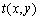
与当前待匹配子集
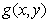
的重叠区域,将其频域内的互功率谱进行Fourier逆变换,得到脉冲函数,通过检测该函数峰值的位置,实现空域内图像二维位移的检测。
设两子集尺寸相同,且
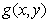
为
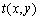
在
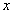
和
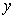
方向分别平移
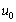
和
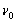
后的位置,即:
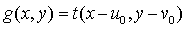
(2)
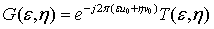
(3)
一般平移不会改变频谱幅度,仅改变相位,进一步计算两者的互功率谱,即
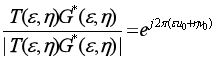
(4)
其中
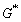
代表
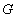
的复共轭。可以看出,互功率谱在频域中的相位相当于引用子集与当前子集在空域中的相位差,于是对该互功率谱进行二维逆傅里叶变换,得到一脉冲函数,其峰值即对应子集在空域中的相对平移量
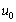
和
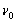
。
理论上FTCC假定两个待匹配子集之间所有数据相同,有效数据周围区域拓延补零,但具体应用到DIC中的FTCC程序,所处理的均是具有部分重叠区域的图像,其余部分为不相关数据。计算仿真表明,FTCC算法要求相关子集之间至少要有大于25%的重叠区域,即
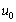
与
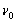
均小于相对应维度的子集尺寸的一半,且重叠区域越高,脉冲峰值越大。这意味着FTCC的搜索范围为子集尺寸的一半。
1.3 DIC亚像素算法
Bruck等
[14]于上世纪八十年代提出了正向累加牛顿拉夫森(Forward additive Newton–Raphson, FA-NR)算法,用于将模板图像快速匹配至目标图像,该算法的核心思想在于迭代优化求局部最优解。潘兵
[15]将IC-GN算法
[16]做了相关改进并将其引入DIC理论,作为一种相对于FA-NR算法,效率更高、鲁棒性更好的DIC亚像素匹配算法。本文基于ZNSSD相关度函数,采用一阶形函数,对DIC中的IC-GN算法进行详细介绍。
采用ZNSSD相关度函数,基于式,定义如下相关度函数
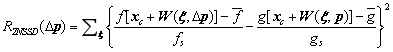
(5)
式中,
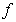
与
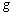
分别为引用子集与目标子集的灰度值,即图 2中引用子集与黄色实线目标区域,
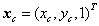
为各子集的中心点坐标的齐次形式。
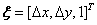
为各子集内像素点到中心点的原始距离。
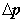
为
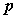
的变化量。
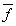
、
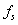
、
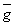
、
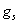
与式中分子、分母项一一对应。
对式基于
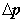
做一阶泰勒展开并舍弃高阶小量,可得
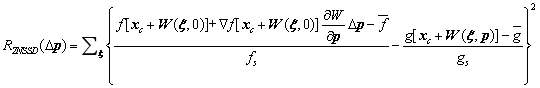
(6)
其中,
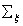
代表全子集区域求和,
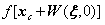
为引用子集
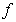
在点
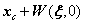
处的灰度值,
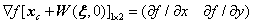
为引用子集
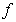
于点
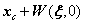
处分别在x与y方向的灰度梯度值,其余参数含义同式。
与传统FA-NR算法
[14]思路相同,若求得式局部极值,即求解
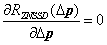
此时有
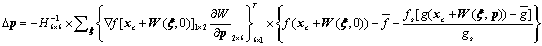
(7)
其中,Hessian矩阵具体形式为
经过式计算后,得到
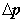
,带入warp函数形成增量warp函数
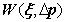
,基于
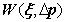
对原
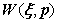
进行更新,即
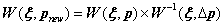
(8)
将
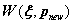
中的
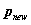
带入式开始新的迭代,迭代终止条件为迭代次数大于10次或欧式距离误差小于0.001。
经过上述迭代过程,IC-GN算法可收敛至局部最优解,该最优解使得式达到局部最小值。与FA-NR相似,一般来讲,迭代初值与正确结果相差几个像素以内,IC-GN算法均能成功收敛至正确的亚像素结果。
通过上述IC-GN计算过程,可以看到,不同于FA-NR,IC-GN算法的每一次迭代运算中,与
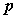
有关的项仅为
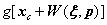
,Hessian矩阵和灰度值梯度项
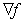
均在迭代开始前计算完成即可,所以IC-GN避免了大部分冗余计算,运算效率高于经典FA-NR算法。基于零阶与二阶形函数的IC-GN算法,原理上没有改变,仅
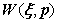
形式以及相关运算矩阵维度发生了变化。基于零阶形函数的IC-GN算法详细推导过程请参考文献[17],基于二阶形函数的IC-GN算法请参考文献[18],其中详细记录了二阶形函数的
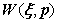
矩阵形式。
1.4 DIC算法分析
亚像素算法迭代收敛与否取决于整像素搜索算法提供的迭代初值是否合理。理想状态下,整像素初值搜索算法所提供的整像素初值结果与正确结果之间的误差不大于0.5个像素,收敛半径一般在几个像素以内。FTCC整像素算法利用引用子集与当前子集的重叠区域,将其频域内的互功率谱进行Fourier逆变换,得到一个脉冲函数,通过检测该函数峰值的位置,实现空域内图像二维位移的检测。
用整像素匹配算法所能达到的检测精度,一般应通过迭代优化型亚像素匹配算法满足测量需求,主要的亚像素算法包括正向算法FA-NR (Forward Additive Newton–Raphson)与反向算法IC-GN两种,由潘兵等人于2013年提出的反向算法IC-GN是在正向算法FA-NR的基础上发展起来,其主要思想就是采用迭代优化的方式求得某个判据的极值,目前普遍采用的判据为零均值归一化最小平方差(zero-mean normalized sum of squared difference, ZNSSD),ZNSSD与ZNCC可互推导,除了具有ZNCC的优势外,其应用于IC-GN中,更易于求导计算。
不同于FA-NR,IC-GN基于参考子集进行迭代计算,省去了FA-NR算法中每次迭代都要进行的Hessian矩阵的计算,从而大大降低了计算量,同时,IC-GN比FA-NR具有更好的鲁棒性。
2 工程应用可行性分析
实际工程中,采用DIC技术进行测试时需要面对各种不同的测试场景,这些测试场景的主要区别在测试距离以及视场宽度,本节内容主要基于民用级数字相机级镜头的具体参数,结合不同的测试距离,对DIC技术进行室外场景测试时的精度进行具体分析,以此来验证DIC技术在土木工程室外测试情景下的可行性。
DIC技术的精度验证主要由硬件参数、理论算法以及测试距离决定,硬件参数方面,主要有分辨率、感光芯片像元尺寸以及镜头焦距等;理论算法方面,通过IC-GN算法可将整像素级别测试精度提高100倍,这也使得DIC技术能够进行高精度测试;测试距离方面,一般在0.5-1000m不等。
基于小孔成像原理,结合相关硬件及拍摄参数,可计算得到测试精度如下:
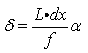
(9)
式中,
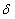
为测试精度,单位为(距离/像素),
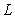
为测试距离,
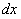
为感光芯片像元尺寸,
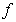
为相机焦距,
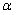
为亚像素精度放大系数。实际测试中,
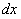
一般可取为2.6
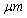
,
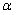
取为0.01,则可得不同焦距与拍摄距离下,DIC技术的理论测试精度,计算结果示于表 1。
同样基于小孔成像原理,结合相关硬件及拍摄参数,可计算得到拍摄视场宽度如下:
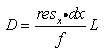
(10)
式中,
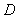
为拍摄视场宽度,单位为公米制实际距离,
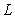
为测试距离,
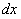
为感光芯片像元尺寸,
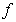
为相机焦距,
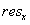
为相机感光芯片横向像素个数。实际测试中,
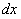
一般可取为2.6
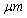
,
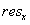
取为1920像素,则可得不同焦距与拍摄距离下,进行DIC测试时的理论视场宽度,计算结果示于表 2。
表 1 不同焦距(mm)与测试距离(m)下的DIC理论测试精度(mm/pixel)
表 2 不同焦距(mm)与测试距离(m)下的DIC测试视场宽度(m)
需要强调的是,表 1与表 2的理论计算结果均基于一般情况下的硬件参数计算得到,实际应用中可通过改变
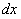
与
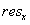
得到更高测试精度与不同的视场范围,尽管如此,表 1与表 2仍具有较强的参考价值。通过表 1数据可以看出,DIC测试精度水平极高,在小焦距、长距离的极端情况下,也可达到毫米级的测试精度。基于表 2数据,结合表 1数据,可以看出,在满足测试精度的前提下,DIC测试的视场范围变动较大,可满足绝大多数的实际室外测试情景。同时,表 1及表 2数据为正对拍摄情形下的理论计算结果,如果是斜对拍摄,则精度会受小孔成像投影影响而有所降低,拍摄视场宽度则会有所增大。
3 工程应用
3.1 苏通大桥电涡流阻尼器运动姿态测试

图 3 苏通大桥电涡流阻尼器运动姿态测试
运用多点数字图像检测系统对苏通大桥电涡流阻尼器的变位视频进行了位移测试。由于一般情况下电涡流阻尼器的变位十分缓慢,肉眼难以察觉,所以该阻尼器变位视频以30fps的帧率,1080p的分辨率对电涡流阻尼器进行长达十分钟的拍摄,拍摄画面以及处理结果示于图 4 (a),现场拍摄的电涡流阻尼器及其支架示于图 4 (b)。
因为电涡流阻尼器的三角结构,所以仅需拍摄其两斜边的刚体位移,就可以把电涡流阻尼器在焦平面内最重要的二维运动姿态通过摄影的方式记录下来,再利用DIC进行跟踪即可。图 4 (a)中阻尼器两斜边上方的蓝点与绿点为追踪目标点,又由于桥面上风速较高,会使得相机产生小幅高频振动,为了消除相机自身振动的影响,在底边横轴上选取了红点作为基准点。最终将两目标点的绝对位移结果减去基准点绝对位移结果,即得到了图 4 (a)中的两条相对位移时程曲线,即阻尼器两斜边相对于底边的相对位移结果。图 4 (b)中的两条位移时程曲线是阻尼器两斜边的竖向位移时程结果,均值化后的曲线极值分别为[-4.49,4.52]mm与[-3.16,4.19]mm,可以看出,该阻尼器在环境激励的位移时程以及运动姿态均可较精确测得。
由于阻尼器变位缓慢,相机以30fps帧率拍摄得到的画面在局部时间内基本处于静止状态,画面稳定,质量较高,此时可将ZNCC阈值适当调高(如
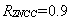
,且因为两帧之间变化缓慢,可采取小参数的FNCC算法结合IC-GN的单点DIC算法,进行阻尼器变位的多点DIC跟踪测试。
3.2 虎门大桥涡振视频跟踪
2020年5月5日下午14时左右,广东省虎门大桥的加劲梁发生明显振动,据网络信息报道,专家初步推测的原因为水马改变了梁体的气动外形。本文基于网络视频(视频素材来源:B767-400ER bilibili),运用多点数字图像检测系统对虎门大桥涡振振幅与频率进行了分析,如图8所示。在图中选择多个密集点进行DIC位移时程跟踪,进而将每一时刻的空间位置点连线,可以得到大桥的振动模态。可以看出,虎门大桥涡振频率较为单一,经过分析,在该视频拍摄时刻,目标点处最大振幅为37cm(简单标定结果),振动频率为0.365Hz,对应虎门大桥第三阶加劲梁竖弯对称振型。
由于该视频较为模糊不清,所以ZNCC阈值设为0.7,运算过程中,采用零阶形函数进行亚像素匹配运算,由于图像画面中的散斑数据稳定但较为模糊,可采取中等尺寸窗口(30×30)参数的FTCC算法结合IC-GN的单点DIC算法。
图 4 DIC密集目标点跟踪结果
4 结论
1)基于理论公式对DIC技术在实际工程应用场景下的测试可行性进行了分析,通过定量分析数据得到,DIC技术在室外场景的拍摄情形下具备较大的测试可行性,DIC测试视场和测试精度均可在一般拍摄条件下达到工程测试需求。
2)基于多点数字图像检测系统进行了苏通大桥电涡流阻尼器运动姿态测试、虎门大桥涡振视频测试等实际土木工程形变测试,实际试验结果证明,DIC形变测试系统具备较高可行性与实用性。
参考文献
[1]. 邵新星, 陈振宁, 戴云彤, et al. 数字图像相关方法若干关键问题研究进展[J]. 实验力学, 2017(3):305-325.
[2]. 叶肖伟, 董传智. 基于计算机视觉的结构位移监测综述[J]. 中国公路学报, 2019, 32(11).
[3]. 晏班夫,李得睿,徐观亚,朱平,邵旭东. 基于快速DIC与正则化平滑技术的结构形变测试;DOI:10.19721/j.cnki.1001-7372.2020.09.019;中国公路学报;2020年第9期;
[4]. Bruck H A, McNeill S R, Sutton M A, et al. Digital image correlation using Newton-Raphson method of partial differential correction[J]. Experimental mechanics, 1989, 29(3): 261-267.
[5]. Sun Y, Pang J H L, Wong C K, et al. Finite element formulation for a digital image correlation method[J]. Applied optics, 2005, 44(34): 7357-7363.
[6]. Réthoré J, Hild F, Roux S. Extended digital image correlation with crack shape optimization[J]. International Journal for Numerical Methods in Engineering, 2008, 73(2): 248-272.
[7]. Pan B, Qian K, Xie H, et al. Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review[J]. Measurement science and technology, 2009, 20(6): 062001.
[8]. Orteu J J. 3-D computer vision in experimental mechanics[J]. Optics and lasers in engineering, 2009, 47(3-4): 282-291.
[9]. Sutton M A, McNeill S R, Helm J D, et al. Advances in two-dimensional and three-dimensional computer vision[M]//Photomechanics. Springer, Berlin, Heidelberg, 2000: 323-372.
[10]. Bay B K, Smith T S, Fyhrie D P, et al. Digital volume correlation: three-dimensional strain mapping using X-ray tomography[J]. Experimental mechanics, 1999, 39(3): 217-226.
[11]. Lewis J P. Fast Normalized Cross-Correlation. Industrial Light & Magic (1995).
[12]. Reddy B.S., Chatterji B.N. An FFT-based technique for translation,rotation,and scale-invariant image registration. IEEE Transactions on Image Processing,1996,5(8):1266~1271
[13]. Pan B, Wang Y, Tian L. Automated initial guess in digital image correlation aided by Fourier–Mellin transform[J]. Optical Engineering, 2017, 56(1):014103.
[14]. Bruck H A, McNeill S R, Sutton M A, et al. Digital image correlation using Newton-Raphson method of partial differential correction[J]. Experimental mechanics, 1989, 29(3): 261-267.
[15]. Pan B, Li K, Tong W. Fast, Robust and Accurate Digital Image Correlation Calculation Without Redundant Computations[J]. Experimental Mechanics, 2013, 53(7):1277-1289.
[16]. Baker S, Mattews I (2004) Lucas-Kanade 20 years on: a unifying framework. Int J Comput Vision 56:221–255.
[17]. Pan B., Tian L, Song X. Real-time, non-contact and targetless measurement of vertical deflection of bridges using off-axis digital image correlation[J]. Ndt & E International, 2016, 79:73-80.
[18]. Gao Y, Cheng T, Su Y, et al. High-efficiency and high-accuracy digital image correlation for three-dimensional measurement[J]. Optics and Lasers in Engineering, 2015, 65: 73-80.
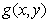 是尺寸为
是尺寸为 像素的搜索区域,也即匹配图像模板。从搜索区域中截取出其中蓝色虚线区域,作为引用子集
像素的搜索区域,也即匹配图像模板。从搜索区域中截取出其中蓝色虚线区域,作为引用子集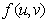 ,引用子集尺寸为
,引用子集尺寸为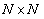 像素,
像素,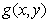 中黄色实线区域尺寸与引用子集
中黄色实线区域尺寸与引用子集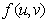 尺寸相同。整像素搜索的核心目标,即定量地找出
尺寸相同。整像素搜索的核心目标,即定量地找出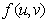 的中心点,在
的中心点,在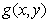 中的整像素坐标
中的整像素坐标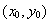 该坐标也就是整像素初值搜索的结果。容易想到,将
该坐标也就是整像素初值搜索的结果。容易想到,将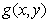 中与引用子集
中与引用子集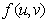 尺寸相同的黄色实线区域,作为目标区域,从左至右、从上到下地逐个像素点遍历全部的
尺寸相同的黄色实线区域,作为目标区域,从左至右、从上到下地逐个像素点遍历全部的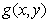 ,在每个遍历路径上的像素点处,将目标区域与
,在每个遍历路径上的像素点处,将目标区域与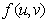 做式的ZNCC运算,即
做式的ZNCC运算,即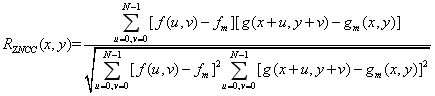
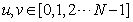 ,
,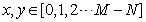 ,
,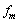 为
为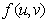 的灰度均值,
的灰度均值,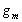 为
为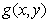 中黄色实线目标区域的灰度均值,
中黄色实线目标区域的灰度均值,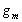 随
随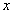 与
与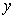 的变化而发生改变。
的变化而发生改变。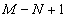 维的
维的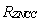 系数方阵,该方阵中,假设
系数方阵,该方阵中,假设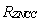 最大值处的坐标为
最大值处的坐标为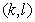 ,则整像素初值搜索结果
,则整像素初值搜索结果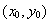 为
为
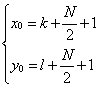
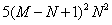 次加法运算与
次加法运算与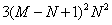 次乘法运算,且计算机乘法运算耗时远大于加法运算。在实际DIC形变测试中,一般有,
次乘法运算,且计算机乘法运算耗时远大于加法运算。在实际DIC形变测试中,一般有,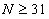 ,
,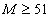 ,式的运算量随着
,式的运算量随着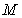 的增大,呈平方倍增长,随着
的增大,呈平方倍增长,随着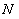 的增大,呈4次方趋势增长。由此可知,式的直接实现方式并非高效。
的增大,呈4次方趋势增长。由此可知,式的直接实现方式并非高效。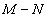 的值代表了搜索范围,
的值代表了搜索范围,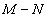 越大,则FNCC的搜索能力越强,但相对应的运算量也就越大,且运算量随着
越大,则FNCC的搜索能力越强,但相对应的运算量也就越大,且运算量随着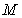 与
与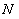 的增大呈非线性快速增长。
的增大呈非线性快速增长。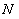 越大则意味着做相关运算的数据越多,也即鲁棒性越强,
越大则意味着做相关运算的数据越多,也即鲁棒性越强,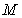 越大则意味着搜索范围越广,增大了受干扰的可能性,也即鲁棒性变差。实际运算时,
越大则意味着搜索范围越广,增大了受干扰的可能性,也即鲁棒性变差。实际运算时,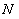 的取值范围一般为15-71,普遍取
的取值范围一般为15-71,普遍取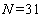 。
。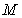 的取值可表示为
的取值可表示为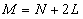 ,
,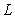 表示搜索范围,单位为像素,
表示搜索范围,单位为像素,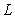 的大小则随测试情况而定。
的大小则随测试情况而定。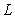 取50也有可能达不到相应的搜索范围要求,且此时FNCC计算量非常大,鲁棒性也受到较大影响。由于土木工程测试情形,普遍具备小位移、慢位移、小旋转的特点,FNCC算法还是能够满足绝大多数土木工程形变测试场景的。在进行高速冲击试验时,则需要运用高速摄像机进行图像的采集,来实现两帧间小位移的条件。
取50也有可能达不到相应的搜索范围要求,且此时FNCC计算量非常大,鲁棒性也受到较大影响。由于土木工程测试情形,普遍具备小位移、慢位移、小旋转的特点,FNCC算法还是能够满足绝大多数土木工程形变测试场景的。在进行高速冲击试验时,则需要运用高速摄像机进行图像的采集,来实现两帧间小位移的条件。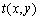 与当前待匹配子集
与当前待匹配子集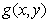 的重叠区域,将其频域内的互功率谱进行Fourier逆变换,得到脉冲函数,通过检测该函数峰值的位置,实现空域内图像二维位移的检测。
的重叠区域,将其频域内的互功率谱进行Fourier逆变换,得到脉冲函数,通过检测该函数峰值的位置,实现空域内图像二维位移的检测。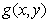 为
为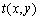 在
在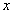 和
和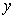 方向分别平移
方向分别平移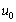 和
和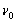 后的位置,即:
后的位置,即:
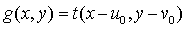 (2)
(2)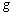 和
和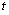 相对应的二维傅里叶变换
相对应的二维傅里叶变换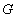 和
和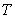 有如下关系:
有如下关系: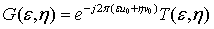 (3)
(3)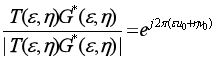 (4)
(4)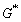 代表
代表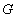 的复共轭。可以看出,互功率谱在频域中的相位相当于引用子集与当前子集在空域中的相位差,于是对该互功率谱进行二维逆傅里叶变换,得到一脉冲函数,其峰值即对应子集在空域中的相对平移量
的复共轭。可以看出,互功率谱在频域中的相位相当于引用子集与当前子集在空域中的相位差,于是对该互功率谱进行二维逆傅里叶变换,得到一脉冲函数,其峰值即对应子集在空域中的相对平移量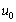 和
和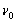 。
。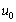 与
与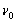 均小于相对应维度的子集尺寸的一半,且重叠区域越高,脉冲峰值越大。这意味着FTCC的搜索范围为子集尺寸的一半。
均小于相对应维度的子集尺寸的一半,且重叠区域越高,脉冲峰值越大。这意味着FTCC的搜索范围为子集尺寸的一半。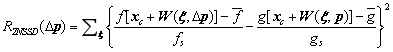 (5)
(5)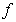 与
与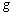 分别为引用子集与目标子集的灰度值,即图 2中引用子集与黄色实线目标区域,
分别为引用子集与目标子集的灰度值,即图 2中引用子集与黄色实线目标区域,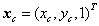 为各子集的中心点坐标的齐次形式。
为各子集的中心点坐标的齐次形式。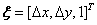 为各子集内像素点到中心点的原始距离。
为各子集内像素点到中心点的原始距离。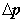 为
为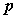 的变化量。
的变化量。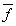 、
、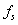 、
、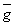 、
、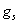 与式中分子、分母项一一对应。
与式中分子、分母项一一对应。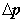 做一阶泰勒展开并舍弃高阶小量,可得
做一阶泰勒展开并舍弃高阶小量,可得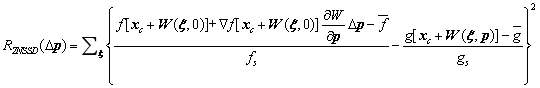 (6)
(6)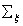 代表全子集区域求和,
代表全子集区域求和,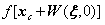 为引用子集
为引用子集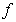 在点
在点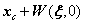 处的灰度值,
处的灰度值,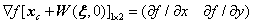 为引用子集
为引用子集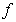 于点
于点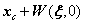 处分别在x与y方向的灰度梯度值,其余参数含义同式。
处分别在x与y方向的灰度梯度值,其余参数含义同式。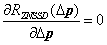
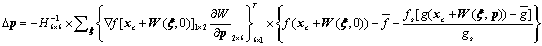 (7)
(7)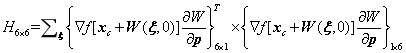
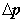 ,带入warp函数形成增量warp函数
,带入warp函数形成增量warp函数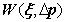 ,基于
,基于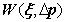 对原
对原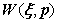 进行更新,即
进行更新,即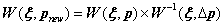 (8)
(8)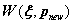 中的
中的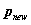 带入式开始新的迭代,迭代终止条件为迭代次数大于10次或欧式距离误差小于0.001。
带入式开始新的迭代,迭代终止条件为迭代次数大于10次或欧式距离误差小于0.001。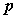 有关的项仅为
有关的项仅为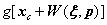 ,Hessian矩阵和灰度值梯度项
,Hessian矩阵和灰度值梯度项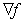 均在迭代开始前计算完成即可,所以IC-GN避免了大部分冗余计算,运算效率高于经典FA-NR算法。基于零阶与二阶形函数的IC-GN算法,原理上没有改变,仅
均在迭代开始前计算完成即可,所以IC-GN避免了大部分冗余计算,运算效率高于经典FA-NR算法。基于零阶与二阶形函数的IC-GN算法,原理上没有改变,仅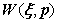 形式以及相关运算矩阵维度发生了变化。基于零阶形函数的IC-GN算法详细推导过程请参考文献[17],基于二阶形函数的IC-GN算法请参考文献[18],其中详细记录了二阶形函数的
形式以及相关运算矩阵维度发生了变化。基于零阶形函数的IC-GN算法详细推导过程请参考文献[17],基于二阶形函数的IC-GN算法请参考文献[18],其中详细记录了二阶形函数的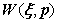 矩阵形式。
矩阵形式。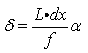 (9)
(9)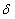 为测试精度,单位为(距离/像素),
为测试精度,单位为(距离/像素),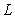 为测试距离,
为测试距离,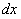 为感光芯片像元尺寸,
为感光芯片像元尺寸,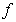 为相机焦距,
为相机焦距,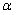 为亚像素精度放大系数。实际测试中,
为亚像素精度放大系数。实际测试中,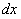 一般可取为2.6
一般可取为2.6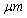 ,
,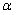 取为0.01,则可得不同焦距与拍摄距离下,DIC技术的理论测试精度,计算结果示于表 1。
取为0.01,则可得不同焦距与拍摄距离下,DIC技术的理论测试精度,计算结果示于表 1。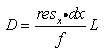 (10)
(10)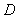 为拍摄视场宽度,单位为公米制实际距离,
为拍摄视场宽度,单位为公米制实际距离,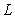 为测试距离,
为测试距离,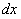 为感光芯片像元尺寸,
为感光芯片像元尺寸,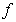 为相机焦距,
为相机焦距,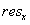 为相机感光芯片横向像素个数。实际测试中,
为相机感光芯片横向像素个数。实际测试中,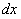 一般可取为2.6
一般可取为2.6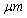 ,
,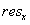 取为1920像素,则可得不同焦距与拍摄距离下,进行DIC测试时的理论视场宽度,计算结果示于表 2。
取为1920像素,则可得不同焦距与拍摄距离下,进行DIC测试时的理论视场宽度,计算结果示于表 2。
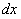 与
与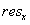 得到更高测试精度与不同的视场范围,尽管如此,表 1与表 2仍具有较强的参考价值。通过表 1数据可以看出,DIC测试精度水平极高,在小焦距、长距离的极端情况下,也可达到毫米级的测试精度。基于表 2数据,结合表 1数据,可以看出,在满足测试精度的前提下,DIC测试的视场范围变动较大,可满足绝大多数的实际室外测试情景。同时,表 1及表 2数据为正对拍摄情形下的理论计算结果,如果是斜对拍摄,则精度会受小孔成像投影影响而有所降低,拍摄视场宽度则会有所增大。
得到更高测试精度与不同的视场范围,尽管如此,表 1与表 2仍具有较强的参考价值。通过表 1数据可以看出,DIC测试精度水平极高,在小焦距、长距离的极端情况下,也可达到毫米级的测试精度。基于表 2数据,结合表 1数据,可以看出,在满足测试精度的前提下,DIC测试的视场范围变动较大,可满足绝大多数的实际室外测试情景。同时,表 1及表 2数据为正对拍摄情形下的理论计算结果,如果是斜对拍摄,则精度会受小孔成像投影影响而有所降低,拍摄视场宽度则会有所增大。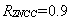 ,且因为两帧之间变化缓慢,可采取小参数的FNCC算法结合IC-GN的单点DIC算法,进行阻尼器变位的多点DIC跟踪测试。
,且因为两帧之间变化缓慢,可采取小参数的FNCC算法结合IC-GN的单点DIC算法,进行阻尼器变位的多点DIC跟踪测试。